小学６年生「分数のわり算」の意味と教え方

　小学６年生の算数の学習に「分数のわり算」があります。ある先生に「どうやって「分数のわり算」を教えたらいいですか」と，質問されました。また，「分数のわり算」の教え方が難しい，という話をよく聞きます。そこで，どのように「分数のわり算」を教えたら子どもが理解できるようになるのか，あるいは子どもにとって分かりやすいのか，自分なりに考えてみました。

　これから私が紹介する方法は，仮設実験授業や水道方式，新居信正さんから学んだものです。間違っている部分あるいは，おかしい部分がある場合は，教えてください。よろしくお願いします。

　「分数のわり算」を教える場合，自然数のわり算と分数や少数のわり算とわり算の意味が大きく違います。まず，そこをはっきりさせたいと思います。

　自然数でのわり算の意味は，文字通り＜分ける＞という意味です。例えば，３人で分けるとか，４個ずつ分けるとか，の意味になります。＜分ける＞という意味について，詳しく説明します。

　自然数による一般的なわり算は，等分除と包含除の２つの意味があります。ひとつずつ考えてみましょう。

例題を解いてみましょう。

計算での答えの求め方は，次のようになります。

３の段のかけ算をして15個になる数が答えです。

例題を解いてみましょう。

計算での答えの求め方は，次のようになります。

３の段のかけ算をして15個になる数が答えです。

　＜小数でわる＞わり算の意味は，１当たり量を求める計算になります。例えば，0.4ｇが2,000円の金があるときに，この金１ｇでは何円になりますか，という問題の場合は，わり算を使います。

式にすると次のようになります。

＜小数でわる＞わり算の意味を説明する前に，＜整数でわる＞わり算の意味について例題で説明します。

１ｍ当たりの金額を求めるためには，８ｍの金額である480円を８ｍでわると，１ｍの値段が求められます。

計算での答えの求め方は，次のようになります。

８の段のかけ算をして480円になる数が答えです。

次に＜小数でわる＞わり算の意味について例題で考えることにします。

この場合も＜整数でわる＞わり算と同じように，次のわり算の式で答えが求められます。

１ｍ当たりの金額を求めるためには，0.2ｍの金額である120円を0.2ｍでわると，１ｍの値段が求められということです。

図で表すと，次のようになります。

ここでは，いきなり120円÷0.2の計算をしないで，解き方を考えてから答えを出してみます。

0.2ｍの何倍が１ｍになるかというと，１ｍ÷0.2ｍ＝５倍

つまり0.2ｍの５倍が１ｍということです。

ということは，１ｍあたりのこの針金の金額は，120円×５＝600円，ということになります。

これを式に表すと，

となります。

　つまり120円を0.2ｍでわると，１ｍの値段が求められるということです。

別の考え方として，

　例えば3.4ｍの長さの針金が1360円であれば，この針金１ｍの値段は，次のように求められます。

１ｍの値段を〇円とすると，

〇円/ｍ×3.4ｍ＝1360円

という式になります。

つまり，

ということは，１ｍの値段は次の式になります。

で答えが求められます。

計算すると，

以上を踏まえて分数のわり算について考えることにします。

　分数のわり算の意味は，小数のわり算の意味と同じです。＜分数のわり算＞の意味は，１当たり量を求める計算になるからです。

例題で考えることにします。

１dl当たりの広さをたずねているので，式は次のようになります。

と，なります。

１dl当たりの広さを求めるためには，広さを〇dlでわり算をすれば求められるからです。

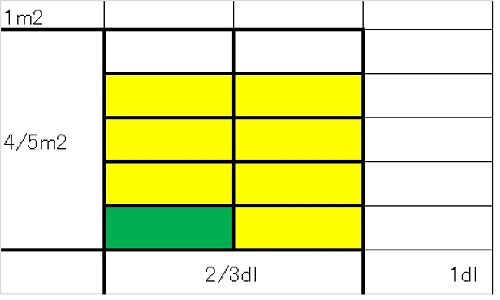
図で表します。

黄色の部分がこの2/3dlのペンキで塗れる範囲です。

次の図は，2/3dlのペンキで4/5m²の広さを塗れるということを黄色で表しています。

次の図の緑色の部分は，1/10m2を表しています。（m2は，平方メートルを表します）

黄色の部分は，8/10m2つまり4/5m2を表しています。（m2は，平方メートルを表します）

このペンキ1dlでは，次の黄色の部分だけ塗ることができます。

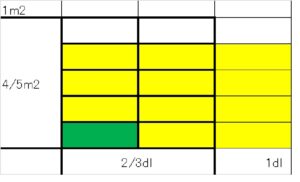
1/10m2が12個あるので，このペンキ1dlで12/10m2塗れることになります。

なので，

つまり，緑色の部分は1/5×1/2 で1/10m2

黄色の部分は　1/10 が4×3 で 緑色の部分が12 個あることになります。

ということは，4/5m2 ÷ 2/3dlの計算は，

4/5 × 3/2の計算をすると答えが出せることになります。

例題３．の式と答えは，次の通りです。

何か，わかったような，わからないような？？？感じなので，別の考え方でお伝えします。

ここでは，計算式だけで分数のわり算をします。

最後に，計算式をボードに書いてまとめます。

おそらく，その方が分かりやすいと考えます。

ここでは，次の２つの式を使います。

　この計算は分かりにくいので，ボードを使って表すと，次のようになります。これで，分かりやすくなったと思いますが，どうでしょうか？

分数÷分数も同じようにできます。

最後に，計算式をボードに書いてまとめてみます。

　この計算についても，分かりやすくするためにボードを使って表すと，次のようになります。

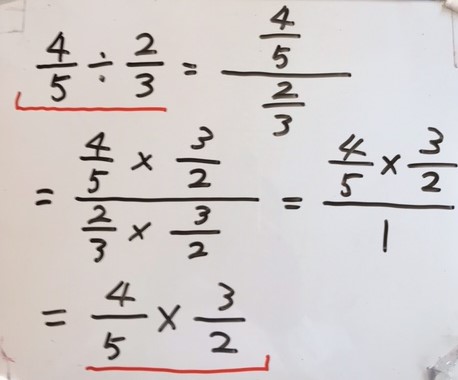
最後に，分数÷分数について簡単な言葉にまとめます。

と，いうことになります。

以上で，私の「分数のわり算」の教え方の説明を終わります。

最後まで読んでいただき，ありがとうございました。

私のおすすめは，兵庫県北部にある湯村温泉です。

小さな温泉地でのんびりできます。

旅館のおすすめは，部屋が広くて，リーズナブルなのはコトブキ（残念ながら露天風呂はありません！），プライベートな空間で食事をして，豪華で大きな露天風呂があるのは朝野家，プールやゲームコーナーがあってリーズナブルなのは井づつや，古い旅館でもいいなら＜とみや＞（笑）

やっぱり「朝の家」最高！（湯村温泉）

→https://tk-s-e-office.com/?p=2880

このプールいいよね！（兵庫県・湯村温泉）

→https://tk-s-e-office.com/?p=2805

旅館の近くには，＜さんそん＞という居酒屋があります。日本酒のソムリエがいておいしい日本酒を飲むならココ！

＜さんそん＞の近くに＜中華料理　笑来園（しょうらいえん）＞があります。ここは，餃子がおいしいです！

＜じゃらん＞では，いろんな種類の宿泊施設を紹介しています。

・犬や猫と一緒に泊まれる宿。

・露天風呂付き客室がある宿。

・リーズナブルな宿。

・市内にある交通の便がとてつもなく便利な宿。

あなたの宿泊条件にピッタリの宿が必ずあります。

お値段の設定もいろいろです。

ぜひ調べてみてください。

よかったら下のサイトからどうぞ。

【じゃらん】国内25,000軒の宿をネットで予約OK！2％ポイント還元！