板倉聖宣著『ぼくらはガリレオ』（岩波現代文庫2011年1月発行）の紹介

板倉聖宣著『ぼくらはガリレオ』（岩波現代文庫2011年1月発行）の紹介

これから，板倉聖宣著『ぼくらはガリレオ』を紹介します。

（写真はガリレオです）板倉さんは，この本の中で次のように書いています。「私（板倉）はこの本を「ゆっくり科学することを楽しみたい」という人たちに読んでほしいと思っています」，つまりこの本は，知識を仕入れるための本ではなく，自分の頭で考えながら読んでほしいということだと思います。

この本は全部で，５つの話から構成されています。今回は，第１話だけの紹介となります。他のお話が気になる方は，ぜひ本書を手にとっていただければと思います。ここで，第２話から第５話までのタイトルだけを紹介しておきます。

• 第２話，真空とものの落ちる速さについて
• 第３話，空気中で落ちるものの速さ
• 第４話，振り子の運動のなぞは落下運動のなぞ
• 第５話，最後の仕上げ

前置きが長くなりました。それでは，第１話を紹介させていただきます。第１話のタイトルは，すりかえられた黄金はどれだけか――アルキメデスとガリレオ――です。

王冠の謎の物語

あなたは「王冠の謎の物語」をご存知でしょうか。今から2200年以上もの大昔，古代ギリシャにアルキメデスという学者がいました。彼は「王冠の謎」を解き明かしたというのです。ここで「王冠の謎の物語」を簡単に説明しましょう。

当時の国王は，細工師に純金の冠（かんむり）を作らせました。できあがってきた冠は，どうも純金ではないらしいといううわさがひろがりました。そのうわさが国王の耳に入ってしまいました。国王はカンカンになって怒りました。うわさ通り王冠が純金でできていないとすると，国王は細工師に騙されたことになります。また，王冠が本物の純金だとすると，「あの王冠は偽物だ」といううわさを流した者の方が国王の権威を傷つけた悪者となってしまいます。そこで，王様はアルキメデスに相談しました。それは，「王冠を壊さずにそれが全部純金でできているか，それとも銀のまぜものがしてあるのか，ということを確かめることができないか」という内容でした。アルキメデスは宿題を与えられたものの，すぐには名案が浮かびませんでした。そして伝説によると，彼はこの問題を考え考え公衆浴場へ行きました。そのとき，風呂の湯は湯舟の上まで満々とたたえられていました。

「ここに入ったら，湯があふれ出してしまって，もったいないな。私の体の大きさの分だけ，流れ出てしまうんだからな。」こう考えるともなく考えて湯舟につかったアルキメデスは，とつぜん「わかった！」と叫びました。そして裸のままで風呂場をとび出して，「わかった！」「わかった！」と叫びながら家に帰ったということです。

言い伝えによると，それからアルキメデスは，この発見（ものを水に入れると，その体積と同じ量の水があふれ出るという発見）にヒントを得て，次のようなことをやってみました。――まずひと塊の純金をとってその重さをはかり，次に銀をそれと同じ重さだけとって，ひと塊にしました。そして，水をいっぱいに満たしたいれものを用意し，銀の塊りを入れてどれだけ水がこぼれ出るかをしらべました。それから金の塊りについても同じことをやってみました。すると，金と銀とでは同じ重さでも，銀の方がずっとたくさんの水をあふれ出させることがわかりました。そこで，いよいよ実際に調べてみました。その結果，同じ重さの純金の塊りのときより，王冠のときの方がずっとたくさんの水をあふれさせることがわかりました。王冠は純金だけでできているのではないことがはっきりとわかったのです。（ヴィトルヴィウス「建築書」第9書序）

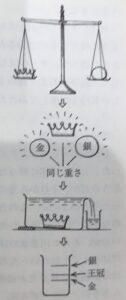
しかしガリレオは，アルキメデスが裸で「わかった，わかった」と叫んで家に帰ったという話までは，無条件に楽しいと思うのですが，それから先の話になると，あまり気に入らなかったということです。というのは，この方法だと，金・銀の塊りや王冠を水の中につけて，あふれ出る水の体積がどれだけか，実際に正確にはかることはたいへん難しいからです。つまり「この方法は実験的に厳密だとは言えない」とガリレオは思ったのです。「ほんとうのアルキメデスは，もっとずっと数学的に厳密にやったにちがいない」というのがガリレオの考えでした。そこで，アルキメデス自身が発見した「てこの原理」と「浮力の原理」を使って，王冠の秘密を正確に解く方法をガリレオは考えはじめました。

あなたも一度，時間をとって「王冠の秘密を正確に解く方法」を考えてみませんか。

ここに「王冠の秘密を正確に解く方法」を書いてみてください。

やがてガリレオ青年はその方法を考え出すのに成功しました。そしてその考えを一つの短い文章――「論文」にまとめることにしました。ガリレオはその論文に「小さなはかり」という表題をつけました。それは，ガリレオ青年がまとめあげた，生まれてはじめての論文でした。

浮力の原理について

それでは，はじめに「浮力の原理」について考えていきましょう。これから，みなさんに「浮力の原理」が理解できるように板倉さんが考えたいくつかの問題を解いてもらいます。早速，ここで問題です。

問題1-1

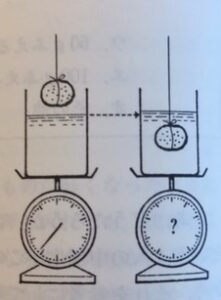
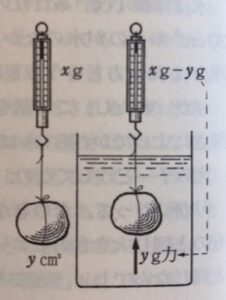
小石を糸でつり下げて，その重さをはかったら，100ｇありました。それから，その石をつり下げたまま水のなかに入れてばねばかりの目盛りを見たら，60ｇになっていました。

このとき，もし水の入ったいれものを，はかりの上にのせておいたら，下のはかりの針はどうなるでしょうか。

予　想

• ア.もとのまま
• イ.40ｇふえる
• ウ.60ｇふえる
• エ.その他

正解は，イ40ｇふえる，になります。つまり，100ｇからばねばかりの目盛りの60ｇを引いた重さの40ｇがふえることになります。当たり前と言えば当たり前です。重さはどこにも逃げないのですから，何かで支えないといけないからです。

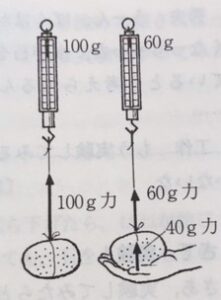
ここで，次のことが気になりました。水の浮力もものの形やものを沈める深さによってちがうかもしれません。そこで，こんな実験をやってみることにします。

ここで，問題です。

問題1-2

糸に石をむすびつけ，ばねにぶら下げたら，ばねが伸びました（このばねはもっと伸ばしても，石をとればもとの長さにもどります）。

ばねにつるした石を，深い水の入れものの中に沈めたら，石をつるしたばねの伸びは空気中のときよりもずっと少なくなりました。

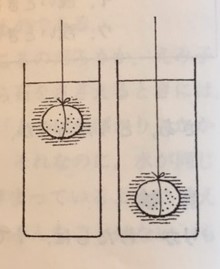
そこで，こんどはこの石を，いれもののうんと深いところに（底につかないように）沈めます。このとき，ばねの伸びはどうなると思いますか。

深いとき（B）のばねの伸びは，

予　想

• ア. 浅いとき（A）よりも短くなる。
• イ. 浅いとき（A）よりも長くなる。
• ウ. 浅いとき（A）とほとんどかわらない。

正解は，ウ. 浅いとき（A）とほとんどかわらない，になります。浮力の大きさはなぜ深さにほとんど関係しないのか，そのことはあとで考えることにします。

ここで，問題です。

問題1-3

ビニール袋に水を入れて，空気の残っているところがないようにしっかり口を閉じて，その重さを量ったら50ｇありました。

この「ビニール袋入りの水」を前と同じようにばねばかりにつるして，全部水のなかに入れたら，ばねばかりはおよそ何ｇのところをさすと思いますか。

予想

• ア.（　　）ｇ
• イ.見当もつかない。

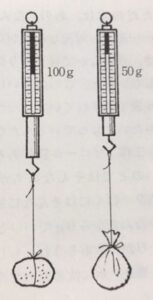
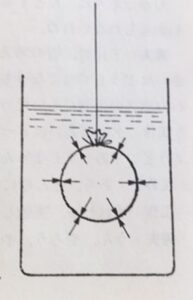
正解は，実験の結果，０ｇになります。みなさんの予想は合っていたでしょうか。よく伸び縮みするばねにビニール袋につめた水をつり下げて水の中に入れていくと，空気中ではどんなに重い水の塊りでも水につけるとその重さがなくなってしまいます。このことは結果がわかってしまうとまったくあたりまえのことのようにも見えますが，これはすばらしい大発見です。これをもとにすれば，「浮力の原理」がよくわかるようになると思います。

ここで，問題です。

問題1-4

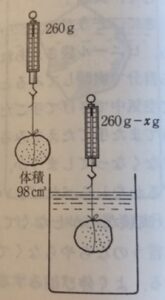
この油粘土の塊りは，体積が98㎤で，重さが260ｇあります。

この油粘土を糸につるして水の中へ入れたら，まわりの水がこの粘土を押し上げる浮力の大きさはどのくらいだと思いますか。

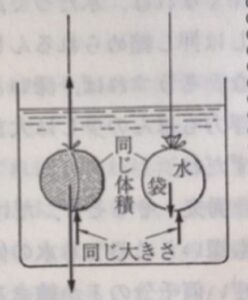
この粘土と同じ体積の水（体積98㎤，重さ98ｇ）をビニール袋に入れて，水の中に入れると，まわりの水は98ｇ分の力（浮力）でビニールの中の水を押し上げようとします。

それでは，同じ大きさの「ビニール袋入りの水」と粘土とでは，浮力の大きさは？

予　想

• ア.同じ
• イ.粘土のときの方が大きい
• ウ.粘土のときの方が小さい

正解は，ア.同じ，です。

「浮力の原理（アルキメデスの原理）」とは・・・

水のなかにものを入れたとき，その物体にはたらく浮力の大きさは，その物体と同じ体積（物体の一部が水面上にとび出ているときは，水面より下の部分の体積）の水にはたらく地球の引力と同じ大きさである。

ものを水に入れるときに，とても深くなれば，水は，ほんの少しは押し縮められます。そうすれば，深いところほど浮力もほんの少しは大きくなると考えられます。だけど数百ｍも深いところでも水の体積はせいぜい何千分の１か縮まるだけでしょう。だから，浮力の大きさは100ｍの深いところでも水面すれすれのところでも，ちがいはせいぜい2000分の１くらいしか違わないと言えるでしょう。

ここで，問題です。

問題２．「浮力の原理」を踏まえて，天秤だけで体積をはかる方法を考えてみてください。あなたは，考えることができますか。

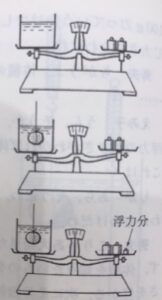
ヒント：次の図を参考にしてください。

正解は，以下の通りです。

まず，天秤の一方の皿の上に水の入ったいれものをのせて，もう一方の皿におもりをのせてつりあわせておきます。次に，その水の入ったいれものの中に，体積を知りたいものをひもでつるして入れます。そうすると，浮力分だけマイナスの重さが皿にかかるから天秤が傾きます。そうしたら，もう一方の皿の上におもりを追加して，何ｇのおもりをのせればつりあうかしらべればよいのです。例えば，10ｇであれば10㎤，23ｇであれば23㎤ということになります。しかも天秤だと0.1ｇや0.01ｇまではかるのは簡単です。浮力が0.1ｇ力なら体積は，0.1㎤ということになります。1㎤の10分の１や100分の１まで正確にはかれるというわけです。これは，すばらしいことです。

王冠の秘密を正確に解く方法とは・・・

ここから，ガリレオが考えた「王冠の秘密を正確に解く方法」を考えてみましょう。それにはガリレオが考えた「小さなはかり」の構造を知ることが大切です。

「小さなはかり」の構造

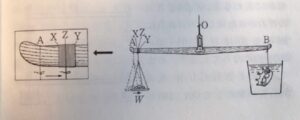
まず，ガリレオの「小さなはかり」のできあがったところを図に示します。この横棒は１ｍ以上の長さのものを使うことになっています。だから，天秤としてはけっして「小さなはかり」などと言うことはできません。けれども，さおばかりとくらべると目盛りを読むところがわずか２～３㎝ぐらいにしかならないから「小さなはかり」というわけです。

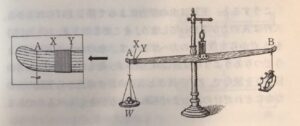
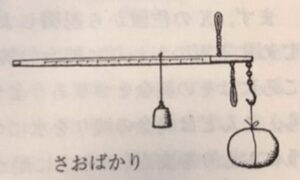
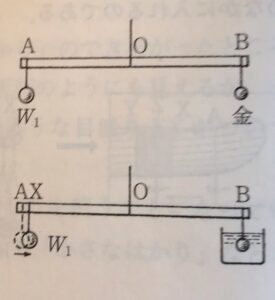
さて，このはかりで，「王冠の金がどれだけの銀ですりかえられているか」をしらべるには，どうしたらよいか，――まず上の図のように，王冠の反対側に王冠と重さのつりあうおもり（Ｗ）をつるしておきます。つぎに，下の図のようにその王冠を水の中に入れます。

こうすると，王冠は水の浮力によって押し上げられるから，天秤はAの方が下がります。そこでこのとき，おもり（Ｗ）をＡ点から視点（Ｏ）の方へずらして，水の中の王冠をちょうどつりあうような位置（Ｚ）に動かします。そしてＸＹのところの目盛りを読んで，ＺＹの長さとＸＺの長さの比から王冠の金の中にどれだけの銀がまぜられているかを調べるのです。

目盛りのつけ方

それなら，XYのところの目盛りは，どのようにしてつけられているのでしょうか。

まず，Xの位置から説明しましょう。これを決めるには，はじめに王冠の代わりに純金の塊りをＢにつるして，Ａのところにはその純金とつりあうようなおもりをつるします。それから，こんどは純金の塊りを水につけて，王冠のときと同じようにおもりを支点（Ｏ）の方に動かしてつりあわせ，ちょうどつりあう点にＸというしるしをつけます。

例えば，はじめの純金の塊りが193ｇあって，おもりＷ1とつりあっていたとします。それを水に入れると，約10ｇ力分の浮力がはたらくので，Ｂ点に加わる力はほぼ193ー10＝183ｇ力になります。そこで，このときおもりＷ1をＡからＸへうごかしてOA：193＝OX：183になるようにしなければならないわけです。もしOAの長さが60㎝だったとするとOXの長さは約69.9㎝，AXの長さは3.1㎝ぐらいということになります。この長さの割合は，最初はかりにかける金塊の大小によってかわることはありません。だからXのしるしをつけるために，はじめにはかりにかける金は王冠の重さと同じである必要はないのです。

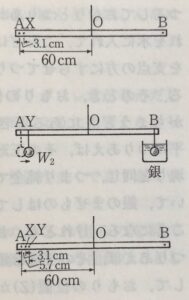
さて，今度はYの位置を決める番ですが，この位置を決めるにはBのところに純金ではなく，純銀をつるします。その銀と重さのつりあうおもりＷ2をＡにつるすことも同じです。そして金のときと同じように銀の塊りを水に入れて，Ｗ2をＡからＯの方に動かして棒が水平につりあうようにした点がＹというわけです。例えば，はじめの銀の重さが210ｇあったとします。それを水に入れると20ｇ力分の浮力がはたらきます。だから，Ｂ点に加わる力は210―20＝190ｇ力分の力になります。そこで，おもりＷ2をＡからＹへ動かしてOA：210＝OY：190になるようにすればよいわけです。OAの長さが60㎝だとすると，OYの長さは約54.3㎝，AYの長さは5.7㎝ぐらいになるでしょう。

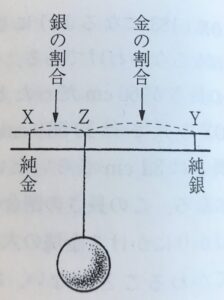
さて，このように，X,Yのしるしをつけておき，王冠をつるしておもりとつりあわせ，それを水に入れて，今度はおもりを支点の方にずらせてつりあわせます。そのとき，おもりの位置（Z）がちょうどXにあるとき棒が水平につりあえば，その王冠は金の塊りと同じ，つまり純金でできていて，銀のまぜものはしていないことになります。けれども，おもりの位置（Z）がYにあったときつりあえば，その王冠は銀だけでできていることになります。そして，おもりの位置（Z）がXとYの間にあってつりあうときは，X側の長さ（XZ）が銀の重さの割合をあらわし，Y側の長さ（ZY）が金の重さの割合をあらわすことになります。つまり，ZがXに近ければその王冠は銀のまぜものが少ないというなるわけです。たとえば，XZの長さがXYの長さの３分の１であれば，その王冠の重さの３分の１は銀だということになります。

目盛りのつけ方と読み方の技術

ガリレオが考えたはかりは，棒の全長が１ｍ以上あっても，肝心の目盛りを読むところが２㎝あまりしかありません。だから，くわしい目盛りをつけて読むことができるように工夫しないと，せっかくのはかりを作ってもあまり正確にはかれないということになってしまいます。

さあ，ここで問題です。

問題３．ガリレオはどうやって目盛りをつけたのでしょうか。次の予想から一つを選んでください。

予　想

• ア.１㎜ごとにペンで印をつけた。
• イ.１㎜ごとに溝を彫った。
• ウ. 針金をつかった。
• エ.その他の考え。

正解は，ウ. 針金をつかった，になります。それでは，ガリレオは針金をつかって，どうやって目盛りをつけたのでしょうか。じつは，ガリレオは，はかりのXとYとの間に細い針金をぎっしりと巻き付けたんです。

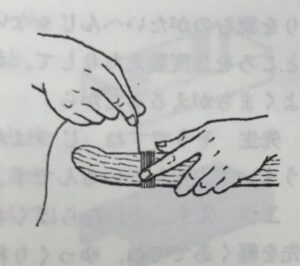
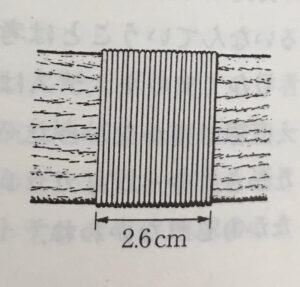
「針金と針金との間にすきまができたり重なりあったりしないように，しっかり巻きつければいい」というわけです。ガリレオの場合は，2.5㎝ぐらいのところに針金を61回ほど巻き付けたようなので，１目盛りが0.4㎜ぐらいにできたわけです。ものさしを使ってペンで印をつけるよりずっと正確で簡単というわけです。

しかし，あなたは気になりませんか。それは，目盛りを読むのがたいへんじゃないか，ということです。あなたは，目がちかちかして，同じところを２度数えるかもしれません。実は，ガリレオもそのことに気づいて，うまい工夫をしているのです。それは，どんな工夫だと思いますか。少し時間をとって考えてみてください。

ガリレオは，コイルの上にペン先を軽くあてて，ゆっくり移動させているのです。そうすれば，ゴトン，ゴトンという手触りと音とで，間違いなく数えることができるのです。

ホッチキスの針がくっついている留め金で一度実験してみるといいと思います。確かに数えることができることを，あなたも実感できると思います。

ガリレオは，理屈ばかりではなく細かい技術的なことまで工夫したのです。「精密に考えるために精密なはかり方も考える」というのが近代科学の一つの特徴とも言えるでしょう。ガリレオは，その先駆者なのです。